What Is Sigmoid Function
The sigmoid function, often represented by the symbol σ, is a mathematical function that maps any real-valued number into a value between 0 and 1. It's commonly used as an activation function in neural networks, particularly in binary classification problems.
Sigmoid Function Definition
The sigmoid function is defined as:
$$\sigma(x) = \frac{1}{1 + e^{-x}}$$
Where:
- $\sigma(x)$ is the output of the sigmoid function.
- $x$ is the input to the function.
- $e$ is Euler's number, approximately equal to 2.71828.
Key Characteristics of the Sigmoid Function

-
S-shaped Curve: The graph of the sigmoid function forms an S-shaped curve, transitioning smoothly from 0 to 1.
-
Output Range: The output of the sigmoid function is always between 0 and 1. This makes it particularly useful for problems where the output is interpreted as a probability, like in binary classification (e.g., determining if an email is spam or not spam).
-
Non-linear: The sigmoid function is non-linear, which is a crucial property for neural networks. This non-linearity allows the network to learn complex patterns.
-
Differentiable: The sigmoid function is differentiable, meaning it has a well-defined derivative. This property is essential for training neural networks using backpropagation, where derivatives are used to update the weights.
Derivative of the Sigmoid Function
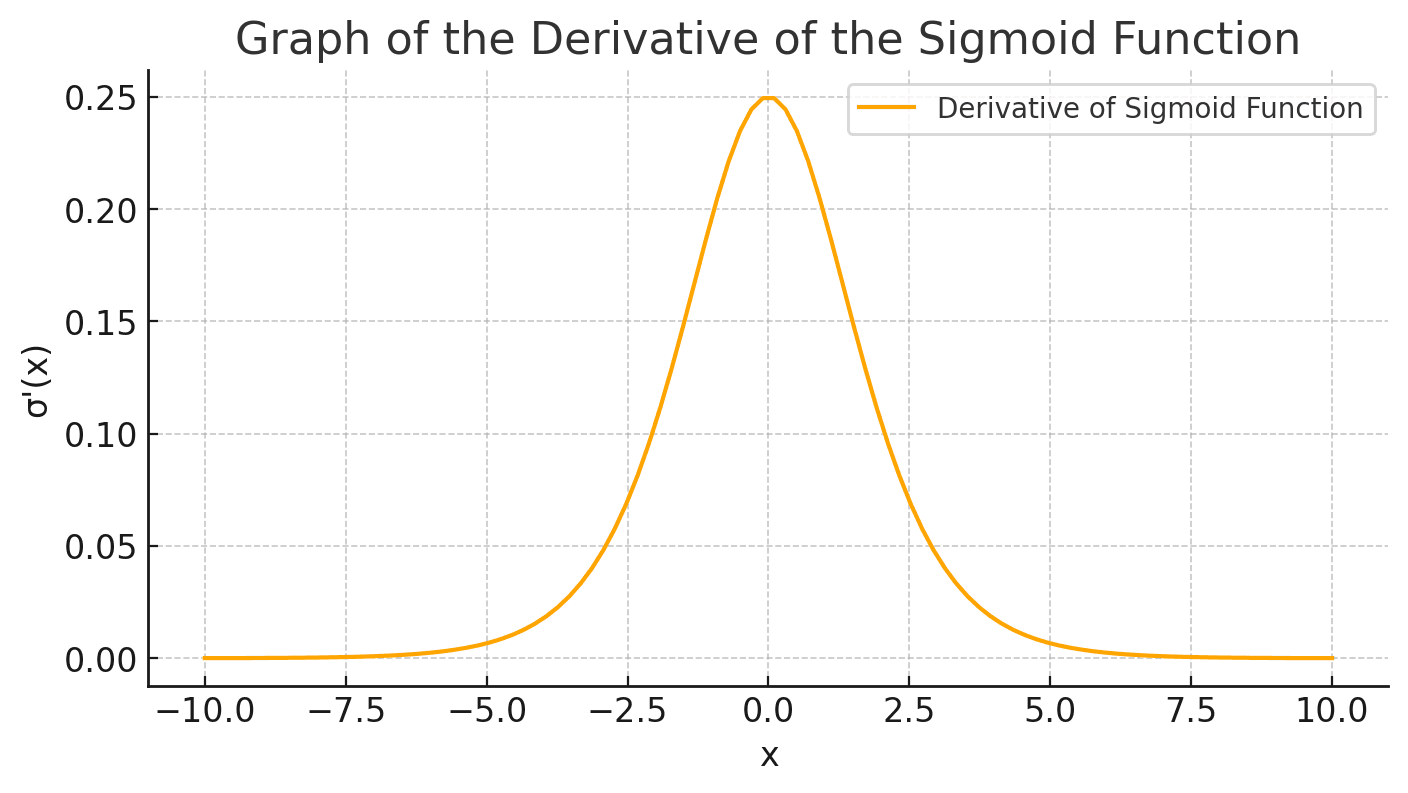
The derivative of the sigmoid function, which is important in the context of neural network training, is given by:
$$\sigma'(x) = \sigma(x) \cdot (1 - \sigma(x))$$
This derivative indicates how the function's output changes with respect to a change in its input, and it plays a pivotal role in the backpropagation algorithm for adjusting weights in the network.
Recent Developments and Considerations
While the sigmoid function has been foundational in the development of neural networks, recent advancements have led to the exploration and adoption of alternative activation functions, such as the ReLU (Rectified Linear Unit) and its variants (e.g., Leaky ReLU, Parametric ReLU). These alternatives often exhibit better performance for deep learning tasks, particularly in deep networks, due to their ability to mitigate issues like the vanishing gradient problem that can arise with the sigmoid function.
Furthermore, the resurgence of interest in explainable AI has prompted researchers to investigate the interpretability of activation functions, including the sigmoid, in the context of model predictions, particularly for binary classification tasks.
While the sigmoid function remains a critical tool in the machine learning toolbox, it is essential to consider the specific requirements of the task at hand and stay abreast of new developments in the field of neural network architectures and activation functions.












